Ohyb na štěrbině s retardační destičkou
Úloha číslo: 1561
Vypočtěte relativní závislost světelné intenzity na úhlu \(\vartheta\) pro Fraunhoferův ohyb na štěrbině šířky \(4D\), přičemž kolem středu štěrbiny je destička šíře \(2D\), která mění fázi dopadající vlny o \(\pi\). Předpokládejte kolmý dopad monochromatické harmonické vlny na štěrbinu, velikost vlnového vektoru je \(k\).
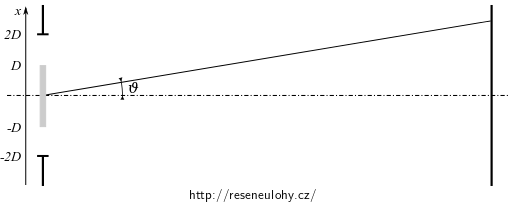
Porovnejte s difrakčním obrazcem jednoduché štěrbiny šíře \(2D\).
Odkaz na podobné úlohy
Jednodušší variantou této úlohy je úloha Ohyb na štěrbině, kde ve štěrbině není umístěna destička.
Teorie a rozbor
• Při výpočtu budeme používat komplexní formalismus, s nímž jsme se seznámili zde a pracovali jsme s ním například v této úloze.
• Štěrbinu budeme předpokládat nekonečně dlouhou.
• Vyzařování štěrbiny budeme modelovat jako spojitý pás přímkových zdrojů harmonických monochromatických válcových vln.
• Máme uvažovat Fraunhoferův ohyb, tj. stínítko ve velké vzdálenosti. Ve velké vzdálenosti je možné válcové vlnoplochy vzhledem ke stínítku malých rozměrů považovat za rovinné.
• Z těchto důvodů budeme interferovat přímo rovinné vlny
\[ E=E_0 e^{i(\omega t - kr + \varphi_0)}, \]kde v amplitudě \(E_0\) je již zahrnut pokles amplitudy válcových vln na cestě ke stínítku tj. tento pokles bude uvažován pro všechny vlny stejný (stínítko je daleko – velmi malé rozdíly drah šíření jsou z tohoto hlediska zanedbatelné).
• Závislost světelné intenzity na stínítku je (v komplexním formalismu) úměrná součinu \[ I \sim EE^\star, \] kde \(^\star\) značí komplexní sdružení.
Nápověda 1 – el. intenzita elementárního zdroje
Napište vyjádření pro elementární příspěvek \(\mathrm{d}E\) elektrické intenzity v daném místě stínítka od elementárního zdroje šířky \(\mathrm{d}x\) na souřadnici \(x\) štěrbiny.
Uvažujte obecnou počáteční fázi \(\varphi_0\).
Nápověda 2 – výpočet integrálu
Elektrická intenzita v daném místě stínítka je dána součtem příspěvků \(\mathrm{d}E\) od všech elementárních zdrojů štěrbiny. Vyintegrujte výraz (2) přes celou štěrbinu. Nezapomeňte, že v centrální části štěrbiny je umístěna destička způsobující změnu fáze!
Nápověda 3 – průběh intenzity na stínítku
Intenzita světla je úměrná výrazu \(EE^\star\), kde \(^\star\) značí komplexní sdružení. Určete tento součin.
CELKOVÉ ŘEŠENÍ – doplnit PO kontrole
• Pro Fraunhoferův ohyb lze válcové vlnoplochy vzhledem ke stínítku malých rozměrů považovat za rovinné vlny ve tvaru
\[ E=E_0 e^{i(\omega t - kr + \varphi_0)}, \]kde v amplitudě \(E_0\) je již zahrnut pokles amplitudy válcových vln na cestě ke stínítku tj. tento pokles bude uvažován pro všechny vlny stejný (stínítko je daleko – velmi malé rozdíly drah šíření jsou z tohoto hlediska zanedbatelné).
• Závislost světelné intenzity na stínítku je (v komplexním formalismu) úměrná součinu \[ I \sim EE^\star, \] kde \(^\star\) značí komplexní sdružení.
Nejdříve najdeme příspěvek k elektrické intenzitě v daném místě stínítka od elementárního zdroje na souřadnici \(x\), který je funkcí času \(t\), vzdálenosti \(r\) místa na stínítku od uvažovaného zdroje a počáteční fáze \(\varphi_0\). Tedy
\[ \mathrm{d}E = \mathcal{E_0} e^{i(\omega t - kr + \varphi_0)} \mathrm{d}x, \]kde konstanta \(\mathcal{E_0}\) má význam elektrické intenzity na jednotku šířky štěrbiny a navíc zahrnuje pokles amplitudy vlny na cestě ke stínítku.
Vzdálenost \(r\) lze vyjádřit z následujích obrázků jako
\[ r= L - x \sin \vartheta. \]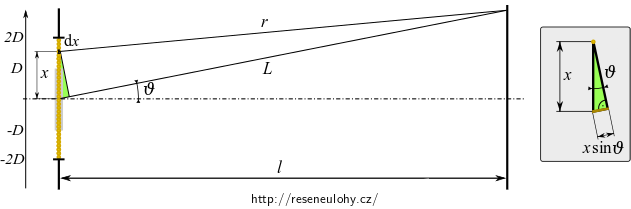
Aproximací pro vzdálené stínítko dostaneme zelený pravoúhlý trojúhelník.
Hledaný příspěvek k elektrické intenzitě v místě stínítka určeném úhlem \(\vartheta\) od elementárního zdroje na souřadnici \(x\) je
\[ \mathrm{d}E = \mathcal{E_0} e^{i(\omega t - kL + kx \sin \vartheta + \varphi_0)} \mathrm{d}x. \]Celkovou el. intenzitu získáme vyintegrováním elementárních příspěvků přes celou štěrbinu
\[ E(\vartheta) = \int\limits_{\small\begin{array}{c}\text{celá}\\ \text{štěrbina}\end{array}} \mathrm{d}E = \mathcal{E_0} e^{i(\omega t - kL)} \left(\, \int\limits_{-2D}^{-D} e^{ikx \sin \vartheta} \mathrm{d}x + \int\limits_{-D}^{D} e^{i(kx \sin \vartheta + \pi)} \mathrm{d}x + \int\limits_{D}^{2D} e^{ikx \sin \vartheta} \mathrm{d}x \right) \]První a třetí integrál představuje části štěrbiny bez retardační destičky, v prostředním integrandu se projeví přítomnost destičky fázovým rozdílem \(\pi\).
a provedeme integraci.
\[ = \mathcal{E_0} \frac{e^{i(\omega t - kL)}}{ik\sin\vartheta} \left( \left[ e^{ikx \sin \vartheta}\right]_{-2D}^{-D}+ \left[ e^{i(kx \sin \vartheta + \pi)}\right]_{-D}^{D}+ \left[ e^{ikx \sin \vartheta}\right]_{D}^{2D} \right) = \] \[ = \mathcal{E_0} \frac{e^{i(\omega t - kL)}}{ik\sin\vartheta} \left( e^{- ik D \sin \vartheta} - e^{- ik 2D \sin \vartheta} + e^{ik D \sin \vartheta} \color{midnightblue}{e^{i\pi}} - e^{- ik D \sin \vartheta} \color{midnightblue}{e^{i\pi}} + e^{ik 2D \sin \vartheta} - e^{ik D \sin \vartheta} \right) = \]\[ = \mathcal{E_0} \frac{e^{i(\omega t - kL)}}{ik\sin\vartheta} \left[ -2\left(e^{ ik D \sin \vartheta} - e^{-ik D \sin \vartheta}\right) + e^{ik 2D \sin \vartheta} - e^{- ik 2D \sin \vartheta} \right] = \]Pomocí Eulerova vztahu \(\color{MidnightBlue}{e^{i\varphi} = \cos\varphi + i\sin\varphi}\) zjistíme, že
\[ \color{MidnightBlue}{ e^{i\pi} = \cos \pi + i\sin \pi = -1, } \] což zjednoduší předchozí výraz..\[ = \mathcal{E_0} \frac{e^{i(\omega t - kL)}}{ik\sin\vartheta} \left( -4i\sin(kD\sin\vartheta) + 2i\sin(2kD\sin\vartheta) \right) = \]K další úpravě využijeme toho, že platí
\[ \color{MidnightBlue}{ e^{i\alpha} - e^{-i\alpha} = 2i\sin\alpha, } \] neboť \[ \small \color{MidnightBlue}{ e^{i\alpha} - e^{-i\alpha} = \cos \alpha + i\sin\alpha - \cos\alpha + i\sin\alpha = 2i\sin\alpha. } \]Při dalších úpravách použijeme goniometrické vzorce a dostaneme hledanou elektrickou intenzitu.
\[ E(\vartheta) = -8D \mathcal{E_0} e^{i(\omega t - kL)} \frac{\sin(kD\sin\vartheta)}{ kD\sin\vartheta} \sin^2\left(\frac{kD\sin\vartheta}{2}\right). \]Dosazením komplexně sdružené elektrické intenzity do vzorce pro světelnou intenzitu dostaneme
\[ I \sim EE^\star = 64 D^2\mathcal{E_0}^2 \underbrace{e^{i(\omega t - kL)}e^{-i(\omega t - kL)}}_{1} \,\frac{\sin^2(kD\sin\vartheta)}{ \left(kD\sin\vartheta\right)^2}\, \sin^4\left(\frac{kD\sin\vartheta}{2}\right). \]Zajímá nás pouze relativní závislost světelné intenzity, tj. hledaná funkce
\[ I\sim \frac{\sin^2(kD\sin\vartheta)}{ \left(kD\sin\vartheta\right)^2}\, \sin^4\left(\frac{kD\sin\vartheta}{2}\right). \]Pro štěrbinu šířky \(2D\) bez destičky by vyšlo pouze (viz úloha Ohyb na štěrbině)
\[ I \sim \frac{\sin^2(kD\sin\vartheta)}{ \left(kD\sin\vartheta\right)^2}. \]Pro porovnání vykreslíme grafy obou předešlých funkcí světelných intenzit do jednoho grafu – žlutě je vynesena situace s destičkou, červeně pak obyčejná štěrbina šířky \(2D\).
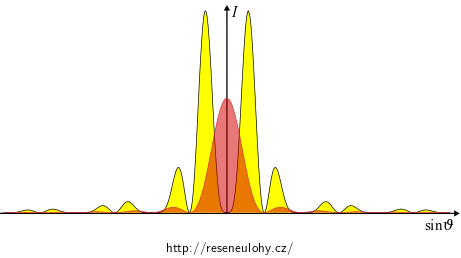
Vidíme, že v případě štěrbiny s retardační destičkou dojde k rozdělení centrálního maxima do dvou částí.
Odpověď
Relativní závislost světelné intenzity na stínítku při ohybu na zadané štěrbině je
\[ I\sim \frac{\sin^2(kD\sin\vartheta)}{ \left(kD\sin\vartheta\right)^2}\, \sin^4\left(\frac{kD\sin\vartheta}{2}\right), \]zatímco při osvětlení štěrbiny šířky \(2D\) bez vložené retardační destičky je závislost jednodušší
\[ I\sim \frac{\sin^2(kD\sin\vartheta)}{ \left(kD\sin\vartheta\right)^2}. \]Hlavním znakem ohybového obrazce štěrbiny s destičkou je rozdělení centrálního maxima na dvě části. Ohybové obrazce pro porovnání jsou na následujícím obrázku (žlutě štěrbina s destičkou, červeně bez):




