Dělič napětí vytvořený z grafitové linky

Pokus číslo: 2192

Cíl pokusu
Cílem pokusu je sestrojit model jednoduchého děliče napětí a demonstrovat na něm princip jeho fungování.
Teorie
Dělič napětí (obr. 1) je název pro jednoduché zapojení, ve kterém můžeme na výstupu (U₁) získat různě velkou část vstupního elektrického napětí U.

Vstupní napětí U se podle Ohmova zákona rozdělí mezi rezistory R₁ a R₂ v poměru jejich odporů. Napětí U₁ lze tedy přímočaře regulovat změnou odporu R₁ – lze odvodit, že pro něj platí:

\[U_{1}=U\frac{R_{1}}{R_{1}+R_{2}}.\tag{1}\]

V tomto experimentu budeme změnu odporu R₁ realizovat tak, že do obvodu zapojíme různě dlouhou část grafitové linky. Přitom budeme předpokládat, že vrstva grafitu je v celé délce linky přibližně homogenní a má stejnou tloušťku – to nám umožní považovat odpor R linky za přímo úměrný její aktuálně zapojené délce l podle vztahu \(R=\rho\frac{l}{S}\), kde S je plocha průřezu linky a \(\rho\) rezistivita.
Odvození vztahu 1
Celkové napětí v obvodu je rovno součtu dvou dílčích napětí:

\[U=U_{1}+U_{2}.\tag{2}\]

Rezistory jsou zapojeny sériově, tedy proud procházející oběma rezistory je stejný. Dílčí napětí lze tedy podle Ohmova zákona vypočítat jako součin proudu v obvodu a jednotlivých odporů:

\[U_{1}=R_{1}I,\tag{3}\]

\[U_{2}=R_{2}I.\tag{4}\]

Vyjádřením proudu ze vztahů (3) a (4) dostaneme:

\[\frac{U_{1}}{R_{1}}=\frac{U_{2}}{R_{2}}\,\Rightarrow\,U_{1}=U_{2}\frac{R_{1}}{R_{2}}.\tag{5}\]

Vyjádříme-li nyní U₂ jako rozdíl vstupního napětí U a výstupního napětí U₁ (ze vztahu (2)), získáme:

\[U_{1}=(U-U_{1})\frac{R_{1}}{R_{2}}.\tag{6}\]

Závěrečné úpravy nám pak dají:

\[U_{1}\left(1+\frac{R_{1}}{R_{2}}\right)=U\frac{R_{1}}{R_{2}},\tag{7}\] \[U_{1}=\frac{\frac{UR_{1}}{R_{2}}}{1+\frac{R_{1}}{R_{2}}}=\frac{UR_{1}}{R_{2}(1+\frac{R_{1}}{R_{2}})}.\tag{8}\]

Nakonec tak získáváme hledaný vztah:

\[U_{1}=U\frac{R_{1}}{R_{1}+R_{2}}.\]
Pomůcky
- voltmetr
- plochá baterie o napětí 4,5 V
- vodiče
- krokosvorky
- tužka s měkkou tuhou
- papír
- pravítko
Postup
1. Na delší stranu papíru A4 či A3 narýsujte pomocí tužky a pravítka několik vodorovných čar tak, aby vytvořily silný grafitový pruh.
2. Změřte napětí baterie U.
3. Pomocí krokosvorek připojte k baterii grafitovou linku (obr. 2).
4. K zápornému pólu baterie připojte uzemněný vstup voltmetru (černý vodič). Druhý vstup voltmetru (volný červený vodič) bude sloužit jako posuvný jezdec.
5. Posouvejte volným vodičem po grafitové lince a pro jeho různé polohy změřte napětí U₁.
Vzorový výsledek
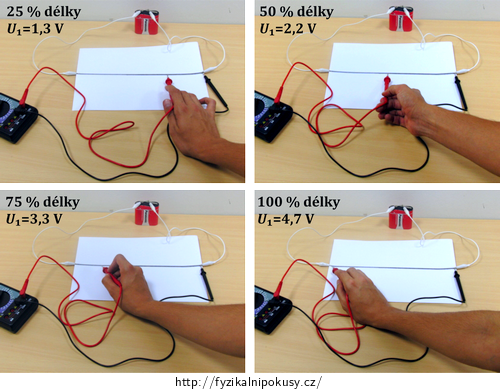
Ve vzorovém provedení experimentu bylo do obvodu postupně zapojeno 25 %, 50 %, 75% a 100 % délky grafitové linky. Tabulka udává napětí U₁ naměřené pro tyto případy.

část linky zapojená do obvodu 25 % 50 % 75 % 100 %

napětí U₁ [V] 1,3 2,2 3,3 4,7

V souladu s výše uvedenou teorií je patrné, že s délkou odporové linky roste napětí U₁, které na děliči naměříme. Tato závislost by měla být podle vztahu (1) dokonce přímou úměrností – je ale patrné, že to rozhodně není splněno ideálně. Zásadní vliv mají samozřejmě nehomogenity grafitové linky, které zapřičiňují, že její stejně dlouhé úseky se svým odporem liší.
Technické poznámky
- Pro výsledek měření je zcela zásadní, aby byla grafitová linka nepřerušovaná a ideálně všude stejně silná. Jen díky tomu pak lze pracovat s předpokladem, že délka linky je úměrná jejímu odporu.
- Reálný dělič napětí je realizován reostatem. Na nevodivém válci je navinut odporový drát s izolací, po navinutí je izolace v jedné linii porušena a po této linii můžeme pohybovat jezdcem, čímž upravujeme velikosti odporů R₁ a R₂.
Metodické poznámky
Se studenty je možné nejdříve provést měření a následně je nechat vymyslet, jak takto navržený dělič napětí vlastně funguje.