Sbírka fyzikálních pokusů

Polovodivost grafitu

Pokus číslo: 4555

• Cíl pokusu

  Cílem pokusu je ukázat polovodivé vlastnosti grafitu, konkrétně pokles elektrického odporu s rostoucí teplotou.

• Teorie

  Závislost proudu \(I\) procházejícího vodičem na úbytku napětí \(U\) na vodiči popisuje Ohmův zákon \[I=\frac{U}{R},\] kde \(R\) je konstanta nazývaná elektrický odpor. Většina vodičů tuto závislost splňuje poměrně dobře, i když odpor ve skutečnosti není konstantní veličina, ale závisí na teplotě vodiče. U vodičů s rostoucí teplotou odpor roste, ale pro malé teplotní rozdíly je tato závislost často zanedbatelná.

  Naopak u polovodičů je závislost na teplotě poměrně výrazná, s rostoucí teplotou jejich odpor klesá. Polovodiče se vyznačují tím, že mají snadno dostupné valenční elektrony, které mohou být uvolněny tepelným pohybem částic v látce − a protože s rostoucí teplotou roste intenzita tepelného pohybu, je uvolnění valenčních elektronů z elektronového obalu snazší. Látka je potom lépe vodivá − má k dispozici více volných nositelů náboje. Látkami vykazujícími polovodivé chování jsou například křemík, germanium, selen, tellur nebo grafit.

• Pomůcky

  Tuha do mikrotužky vyžíhaná v plameni (ve vzorovém provedení tuha tvrdosti HB o tloušťce 0,7 mm a délce 60 mm), 2 multimetry, vodiče, 2 krokosvorky (ideálně připevněné na destičku na délku tuhy od sebe), regulovatelný zdroj stejnosměrného napětí.

• Vyžíhání tuhy v plameni

  Vyžíhání tuhy v plameni je vhodné kvůli odstranění vosku a oleje, které obsahuje její povrchová úprava. Provedení je ukázáno na videu níže. Tuhu vezmeme za okraj do kleští a vložíme do plamene. Příměsi z povrchové úpravy tuhy vzplanou, čímž se jich zbavujeme. Když už tuha pouze žhne, ale nehoří, je vyžíhání hotové.

• Postup

  1. Vyžíhanou tuhu uchytíme na obou koncích do krokosvorek.

  2. Tuhu přes krokosvorky připojíme k regulovatelnému zdroji stejnosměrného napětí a do obvodu zapojíme multimetry jako ampérmetr a voltmetr, viz obr. 1.

  

  3. Postupně zvyšujeme napětí zdroje od 0 V do cca 2 V, zhruba po 0,2 V nebo 0,25 V. Není vhodné příliš překračovat proud 1,5 A, protože pak už je tuha hodně zahřátá a mohla by se přepálit. Naměřené hodnoty proudu a napětí si zaznamenáváme.

  4. Z naměřených hodnot vyneseme do grafu ampérvoltovou charakteristiku (závislost proudu na napětí).

  5. Prvních několik hodnot proložíme přímkou (přímou úměrou).

• Vzorový výsledek

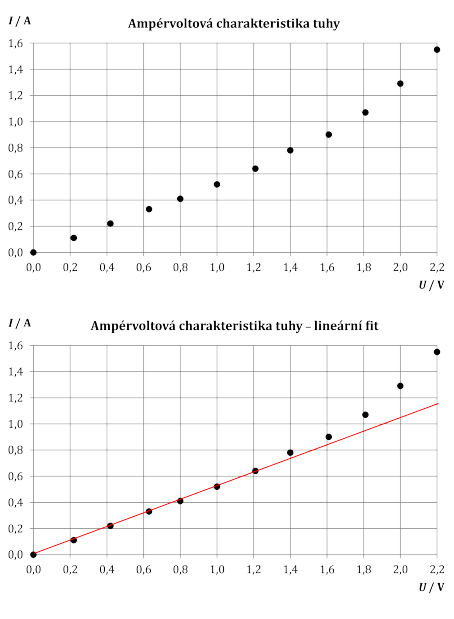
  V grafech níže je vzorová naměřená ampérvoltová charakteristika a proložení prvních 6 bodů (tedy první poloviny bodů) přímkou.

  

  Pro napětí vyšší než přibližně 1,4 V se naměřené hodnoty odchylují od předpovědi z Ohmova zákona znázorněné přímkou. Zvyšování proudu (způsobené zvyšováním napětí) způsobovalo zahřívání tuhy. Při vyšších teplotách byl naměřený proud vyšší, než by při daném napětí odpovídalo materiálu s konstantním odporem (popsanému Ohmovým zákonem). Odpor se tedy s rostoucí teplotou snižoval. Grafit tedy vykazoval polovodivé chování.

• Technické poznámky

  • Při upevňování tuhy do krokosvorek je potřeba postupovat opatrně, protože okraje tuhy jsou po vyžíhání křehké a snadno se lámou. Ideální je upevnit tuhu do obou krokosvorek zároveň.

  • Ampérmetr je vhodné nastavit na rozsah do 2 A a voltmetr na rozsah do 2 V (nebo později do 20 V, pokud budeme měřit do napětí vyššího než 2 V).

  • Při proměřování ampérvoltové charakteristiky je vhodné začít od nižších napětí a postupovat k vyšším a ne naopak, protože tuha se s vyšším procházejícím proudem zahřívá rychleji než pak chladne, když se proud snižuje. Při obráceném postupu by tak výsledky byly méně přesné.

• Doplňující úkol

  Experiment je možno rozšířit výpočtem rezistivity grafitu při pokojové teplotě.

  Z lineárního fitu vyčteme směrnici přímky. Ta je z Ohmova zákonu převrácenou hodnotou odporu (při pokojové teplotě). Odpor závisí na parametrech vodiče podle vztahu \[R=\rho\frac{l}{S},\] kde \(\rho\) je rezistivita materiálu vodiče, \(l\) délka vodiče a \(S\) plocha jeho průřezu daná vztahem \(S = \pi r^2\), kde \(r\) je poloměr vodiče. Z tohoto vztahu tedy můžeme vyjádřit rezistivitu jako \[\rho=\frac{R \pi r^2}{l}.\]

  Ve vzorovém provedení byla směrnice přímky proložené prvními 6 body přibližně 0,52 A/V, čemuž odpovídá odpor R = 1,92 Ω. Délka tuhy zapojené do obvodu byla asi l ≈ 50 mm a její poloměr r = 0,35 mm. Po dosazení tedy dostáváme, že ve vzorovém provedení vycházela rezistivita tuhy při pokojové teplotě ρ ≈ 15 μΩm. Samotný grafit krystalizuje ve vrstvách, takže se narozdíl od tuhy chová velmi anizotropně. Tabulky uvádějí rezistivitu grafitu ve směru vrstev přibližně 1 μΩm a ve směru kolmém na vrstvy přibližně 10 000 μΩm. Tuha se vyrábí z grafitového prášku, takže jsou v ní jednotlivá grafitová zrna různě orientována a výsledná hodnota rezistivity se nachází někde v uvedeném rozmezí. V profesionálních měřeních rezistivity grafitových elektrod (také vyráběných z grafitového prášku) byla její hodnota při pokojové teplotě asi 10 μΩm. Lze diskutovat také odpor přívodních vodičů, přechodové odpory, příměsi grafitu v tuze atd.