Závislost odporu drátu na jeho parametrech

Pokus číslo: 965

Cíl pokusu
Experiment ověřuje závislost odporu vodiče na jeho geometrii (délce, průřezu a materiálu vodiče). Součástí eperimentu je i problémová úloha.
Teorie
Odpor vodiče závisí na jeho délce, ploše průřezu a materiálu vztahem:
\[R = \rho\frac{l}{S},\tag{1}\]
kde ρ je měrný elektrický odpor vodiče, l je jeho délka a S obsah průřezu.

Měrný elektrický odpor (používá se i název rezistivita) vodiče z konkrétního materiálu najdeme v MFCHT. Mezi nejlepší vodiče patří např. stříbro, měď, zlato, atd. Mezi špatné vodiče lze zařadit např. kanthal, konstantan, uhlík a další. Jednotka měrného elektrického odporu plyne z výše uvedeného vztahu (1) po vyjádření ρ:
\[\rho=\frac{R\cdot S}{l},\tag{2}\]
proto
\[\left[\rho\right]=\frac{\Omega\cdot \mathrm{m}^2}{\mathrm{m}}=\Omega\cdot \mathrm{m}\tag{3}\]
Drátům vyrobeným z materiálu s velkým měrným odporem se říká odporové dráty. Jejich rezistivita se pohybuje od cca 0,42·10⁻⁶ Ω·m (nikelin) po např. 1,4·10⁻⁶ Ω·m (kanthal).

Poznámka: Vztah (1) platí přesně pro vodič válcového tvaru, v němž teče proud ve směru jeho osy, což však běžný drát bez problémů splňuje.
Pomůcky
- odporový drát
- měřítko délky alespoň 1 metr
- ohmmetr
- spojovací vodiče, krokosvorky
- případně nůžky a izolepa
Postup
1. Délku drátu postupně zvětšujte s krokem 10 cm a ohmmetrem měřte jeho odpor; přitom dbejte na dobré uchycení drátu ke krokosvorkám.
2. Výsledné hodnoty vyneste do grafu závislosti odporu na délce.
3. Změřte průměr vodiče a pomocí vztahu (2) určete měrný odpor drátu. Hodnotu porovnejte s hodnotou udanou v MFCHT.
Vzorový výsledek
Pro měření byl použit kanthalový drát o délce 0,9 m a průřezu 0,7×0,1 mm (pracovali jsme tedy s drátem, jehož průřez nebyl kruhový, ale obdélníkový). Naměřené hodnoty jsou uvedeny v tabulce:

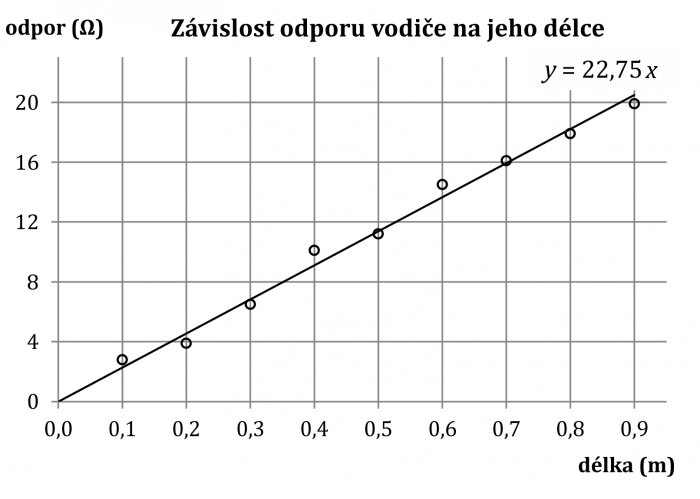
délka drátu (m) odpor drátu (Ω)

0,1 2,8

0,2 3,9

0,3 6,5

0,4 10,1

0,5 11,2

0,6 14,5

0,7 16,1

0,8 17,9

0,9 19,9

Pokud naměřené hodnoty odporu vyneseme do grafu, směrnice proložené přímky nám udá odpor jednoho metru drátu.

Odpor jednoho metru použitého drátu je přibližně 22,8 Ω.

Ze vztahu pro měrný elektrický odpor drátu (2) dostaneme dosazením naměřených hodnot:
\[ \rho = \frac{22{,}75 {\cdot} 7 {\cdot} 10^{-8}}{1} \Omega\cdot\mathrm{m} = 1{,}59{\cdot} 10^{-6}\;\Omega\cdot\mathrm{m}\]
Pro srovnání, tabulková hodnota rezistivity kanthalu je 1,4 μΩ·m.

Rozdíl mezi naměřenou a tabulkovou hodnotou je způsoben převážně přechodovým odporem mezi krokosvorkami a odporovým drátem.
Technické poznámky
- Při provádění experimentu je potřeba si dát pozor na přechodové odpory mezi krokosvorkami a drátem – dbejte na správné uchycení krokosvorek, případně očistěte zoxidovaný povrch drátu smirkovým papírem.
- Experiment je třeba provádět s odporovým drátem, měrný odpor měděného vodiče je příliš malý.
Problémová otázka - přepůlený drát
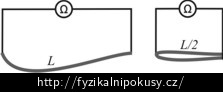
Rozmyslete si, jaký bude odpor drátu, pokud ho přepůlíme a budeme měřit odpor obou polovin tak, jak je to naznačeno na obr. 3:
Přepůlený drát - řešení
Řešení je zřejmé ze vztahu (1) – přepůlený drát má poloviční délku a dvojnásobný průřez, jeho odpor proto bude čtvrtinový. V našem případě vychází odpor 5,6 Ω.
Související výpočetní úloha
Experiment lze propojit s úlohou Elektrický odpor různě dlouhých vodičů.