Sbírka fyzikálních pokusů

Experimentální určení měrné tepelné kapacity vody

Pokus číslo: 1619

• Cíl pokusu

  Cílem tohoto měření je experimentální určení měrné tepelné kapacity vody a její následné porovnání s tabulkovou hodnotou.

• Teorie

  Základní informace o měrné tepelné kapacitě jsou uvedeny v části Porovnání měrné tepelné kapacity oleje a vody, Teorie. Připomeňme pouze, že známe-li měrnou tepelnou kapacitu c látky o hmotnosti m, která se ohřála (ochladila) o Δt, můžeme teplo Q dodané (odebrané) látce vyjádřit jako:

  \[Q\,=\,cm\Delta t.\tag{1}\]

  V tomto experimentu budeme vodu zahřívat průchodem elektrického proudu topnou spirálou. Jestliže takovou spirálu připojíme ke zdroji napětí U a necháme jí po dobu τ procházet elektrický proud I, vykoná se ve spirále eletrická práce W_e, pro kterou platí:

  \[W_\mathrm{e}\,=\,UI\tau.\tag{2}\]

  Pokud zahříváme střídavým proudem, jsou U a I jeho efektivní hodnoty.

  Při průchodu proudu se topná spirála zahřívá a předává teplo vodě a vnitřní nádobě kalorimetru (vnější nádoba je od vnitřní izolována polystyrenovou vložkou, její ohřev tedy nemusíme uvažovat). Protože platí zákon zachování energie, musí být elektrická práce vykonaná na spirále W_e rovna celkovému dodanému teplu, matematicky zapsáno:

  \[ W_\mathrm{e}\,=\,Q_\mathrm{v} + Q_\mathrm{k},\tag{3}\]

  kde Q_v je teplo dodané vodě a Q_k teplo dodané kalorimetru. Na základě vztahu (1) nyní můžeme tepla ve vztahu (3) rozepsat a získáváme:

  \[ W_\mathrm{e}\,=\,c_\mathrm{v}m_\mathrm{v}\Delta t\,+\,c_\mathrm{k}m_\mathrm{k}\Delta t,\tag{4}\]

  kde c_v a c_k jsou měrné tepelné kapacity vody, resp. materiálu, z něhož je vyrobena vnitřní nádoba kalorimetru, a m_v a m_k hmotnost vody, resp. vnitřní nádoby kalorimetru. Zvýšení teploty Δt je stejné pro vodu i kalorimetr, protože pokud není zahřívání extrémné rychlé, jsou tyto objekty v tepelné rovnováze.

  Závěrem už zbývá dosadit do rovnosti (4) ze vztahu (2) a vyjádřit hledanou měrnou tepelnou kapacitu vody:

  \[c_\mathrm{v}\,=\,\frac{W_\mathrm{e}\,-\,c_\mathrm{k}m_\mathrm{k}\Delta t}{m_\mathrm{v}\Delta t}\,=\,\frac{UI\tau\,-\,c_\mathrm{k}m_\mathrm{k}\Delta t}{m_\mathrm{v}\Delta t}.\tag{5}\]

  Vztah (5) nám tak jasně dává informaci o tom, které veličiny je při výpočtu měrné tepelné kapacity třeba určit.

• Pomůcky

  Kalorimetr s topnou spirálou (obr. 1), ampérmetr a voltmetr (stejně mohou posloužit dva multimetry), teploměr (s výhodou podporovaný počítačem), zdroj střídavého napětí, váhy.

  

• Postup

  1. Odvážíme si 100 g vody (hmotnost m_v). Dále zvážíme vnitřní hliníkovou nádobu kalorimetru (hmotnost m_k) a nalijeme do ní uvedených 100 g (tj. cca 100 ml) vody.

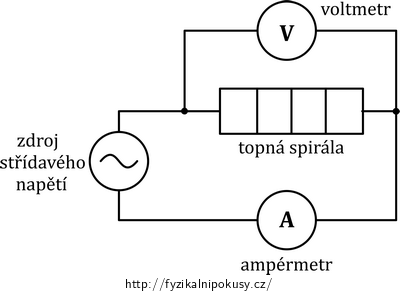
  2. Zapojíme topnou spirálu kalorimetru do obvodu se zdrojem střídavého napětí, ampérmetrem a voltmetrem (schéma elektrického obvodu ukazuje obr. 2, fyzické uspořádání experimentu obr. 3).

  

  3. Zvolíme (stále při vypnutém zdroji!) takovou kombinaci napětí zdroje a odporu spirály, aby obvodem při měření protékal proud přibližně 2 A (ve vzorovém měření například 24 V a 12 Ω).

  4. Ještě než zapneme zdroj, změříme počáteční teplotu vody v kalorimetru; teploměr v něm necháme umístěný po celou dobu měření.

  5. Zapneme zdroj a současně začneme měřit dobu průchodu proudu obvodem. Poznamenáme si také hodnotu napětí a proudu v obvodu.

  6. Po zhruba 3 až 4 minutách zdroj vypneme, vodu rychle promícháme vestavěným míchadlem a odečteme její koncovou teplotu. Nezapomeneme si poznamenat čas τ ohřevu.

  

• Vzorový výsledek

  Následující tabulka shrnuje sedm vzorových měření provedených pro různé kombinace doby ohřevu τ, hmotnosti vody m_v a teplotního rozdílu Δt. Zbylé veličiny byly ve všech měřeních neměnné, a to:

  \(c_\mathrm{k}\,=\,896\,\mathrm{J{\cdot}kg^{-1}{\cdot}K^{-1}}\)

  \(m_\mathrm{k}\,=\,0{,}031\,\mathrm{kg}\)

  \(U\,=\,25{,}9\,\mathrm{V}\)

  \(I\,=\,1{,}85\,\mathrm{A}\)

  Měrná tepelná kapacita byla dopočítávána podle vztahu (5).

  č.měř.	mv (kg)	τ (s)	Δt (°C)	cv (\(\mathrm{J{\cdot}kg^{-1}{\cdot}K^{-1}}\))
  1	0,110	180	17,0	4360
  2	0,103	200	19,8	4440
  3	0,110	200	18,8	4380
  4	0,108	190	18,5	4310
  5	0,104	210	20,6	4430
  6	0,095	195	20,4	4530
  7	0,111	185	17,0	4440

  Průměrná zjištěná hodnota měrné tepelné kapacity vody činí \(c\,=\,(4410\,\pm\,70)\,\mathrm{J{\cdot}kg^{-1}{\cdot}K^{-1}}\), tabulková hodnota při teplotě 25 °C přitom činí přibližně \(4180\,\mathrm{J{\cdot}kg^{-1}{\cdot}K^{-1}}\); odchylka měření představuje asi 5 % této hodnoty.

• Technické poznámky

  • Před zaznamenáním koncové teploty je skutečně nezbytné vodu v kalorimetru promíchat; v opačném případě můžeme získat velmi zkreslené výsledky. Na základě zkušeností autora pokusu je vhodné míchat po celou poslední minutu měření.

  • Použití teploměru, který je možné připojit k počítači, může vést ke značnému zpřesnění výsledků zejména tehdy, je-li doba ohřevu krátká a nárůst teploty v důsledku toho malý.

• Metodické poznámky

  • Rovnost (3) představuje jakýsi ideální případ, který neuvažuje například ohřev okolního vzduchu, ohřev polystyrenové izolace kalorimetru, kondenzaci části vody na spodní straně krytu kalorimetru a další tepelné ztráty. V praxi se z ní se tedy stává nerovnost ve tvaru:

    \[W_\mathrm{e}\,\gt\,Q_\mathrm{v}\,+\,Q_\mathrm{k}\]

    Jinými slovy, účinnost přeměny elektrické energie na tepelnou není stoprocentní. Z tohoto důvodu vychází ve výpočtech hodnoty měrné tepelné kapacity systematicky větší, než je tabulková hodnota \(4180\,\mathrm{J{\cdot}kg^{-1}{\cdot}K^{-1}}\).

  • Fyzikálně zdatnější studenti mohou namítat, že při intenzivním míchání vody v kalorimetru konáme mechanickou práci, což může vést k zahřívání vody uvnitř. Tato myšlenka je principiálně správná a zaslouží ocenění, přestože vliv takovéhoto zahřívání na výsledek měření je prakticky nulový. Chceme-li o tom studenty přesvědčit, můžeme je nechat odhadnout jejich mechanický výkon při míchání a porovnat ho s elektrickým výkonem topné spirály.

• Odkaz na související úlohu

  Výpočetní úloha, která pracuje s kalorimetrickou rovnicí, je Ohřev vody ve varné konvici.