Regelace ledu
Pokus číslo: 2027
Cíl pokusu
Tento experiment ukazuje a popisuje regelaci ledu, jev, při kterém kusem ledu prochází struna, na níž je zavěšené závaží. Poté, co struna ledem projde, zůstává led v kuse.
Teorie
Vyndáme-li z mrazáku kus ledu, bude se pomalu zahřívat, dokud nedosáhne teploty 0 °C. Led taje postupně od povrchu, kterým pomalu přijímá skupenské teplo tání. Povrch ledu je pokryt velmi tenkou vrstvou vody, přičemž teplota na rozhraní ledu a vody zůstává 0 °C.
Teplota tání ledu klesá s rostoucím tlakem. Tlak způsobený strunou má za následek, že teplota tání ledu těsně pod strunou klesne pod 0 °C (v našich podmínkách to bylo asi −0,48 °C (viz komentář) ). Protože teplota ledu je stále 0 °C, led přímo pod strunou taje a struna se pohybuje dolů ve vodě, která vzniká. Zatímco led taje, přijímá skupenské teplo tání z okolí struny a teplota v tomto místě klesne značně pod 0 °C. Toto způsobí, že voda, která je nyní nad strunou a už není pod zvýšeným tlakem, znova zamrzne. Tím se uvolní skupenské teplo tání a teplota v okolí tohoto místa se opět zvýší na 0 °C. Tyto kroky se opakují, dokud struna zcela neprojde skrz celý kus ledu.
Pomůcky
PET lahev
voda
nůž
kovová kytarová struna (pro tento pokus je nejvhodnější struna E1)
kevlarové vlákno
kbelík
závaží

Postup
PET lahev naplníme vodou a necháme ji zmrznout.
Po několika hodinách lahev rozřízneme a vyndáme z ní led.
Umístíme vedle sebe dva stoly tak, aby mezi nimi byla mezera asi 10 cm široká. Led položíme na tyto stoly, střed lahve umístíme nad mezeru. Je vhodné položit led např. na utěrku či ručník.
Přes led vedeme kytarovou strunu, která je připevněna ke kbelíku tak, aby jeho dno viselo asi 30 cm nad podlahou. Do kbelíku vložíme 6 - 7 kg závaží.
Sledujeme, jak struna pomalu prochází ledem a led nad strunou opět zamrzá.
Vzorový výsledek
Při tomto pokusu jsme používali kytarovou strunu o průměr 0,24 mm a kevlarové vlákno o průměru 0,30 mm. Regelace s kevlarovým vláknem probíhala déle než s kytarovou strunou nejen kvůli větší tepelné vodivosti struny, ale také proto, že kevlarové vlákno mělo větší průměr než kytarová struna. Tlak kevlarového vlákna na led byl proto menší než tlak kytarové struny a teplota tání ledu pod kevlarovým vláknem byla vyšší než teplota tání ledu pod kytarovou strunou.
Technické poznámky
Při přípravě ledu neplňte vodou celou PET lahev. Při zamrzání roste objem vody a pokud byste lahev zcela naplnili vodou, mohla by prasknout.
Chystáte-li tento pokus, je lepší vyndat led z mrazáku asi 20 min – 1 hodinu předem. Led bude mít vyšší teplotu, než měl ihned po vynání z mrazáku a regelace bude probíhat rychleji. Při natáčení videa jsme led vyndali přibližně 30 minut před začátkem pokusu a trvalo 10 minut, než kytarová struna prošla ledem.
Metodické poznámky
Pokud budete tento pokus ukazovat s kytarovou strunou i kevlarovým vláknem, měly by mít přibližně stejný průměr, aby pokus probíhal za podobných podmínek. Kytarová struna, kterou jsme používali, měla průměr 0,24 mm, kevlarové vlákno mělo průměr 0,30 mm.
Komentář - teplota tání ledu při zvýšeném tlaku
Zápis
m = 6,5 kg hmotnost závaží zavěšeného na struně d = 2,4·10−4 m průměr kytarové struny l = 5,6·10−2 m průměr ledu v místě, na které shora tlačí kytarová struna Tabulkové hodnoty
lt = 334 kJ·kg−1 měrné skupenské teplo tání ledu ρV = 999,8 kg·m−3 hustota vody při teplotě 0 °C ρL = 916,8 kg·m−3 hustota ledu při teplotě 0 °C T = 373,15 K teplota tání ledu 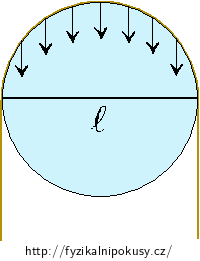
Na obrázku je z názorněn průřez ledem, na kterém je zavěšena kytarová struna. Struna tlačí kolmo na led, při výpočtu proto uvažujeme jen průmět tlakových sil, kterými působí struna, do svislého směru.
Délka l se v průběhu zařezávání ledu zmenšuje a tlak roste. Dále budeme počítat změnu teploty tání na začátku zařezávání.
Při výpočtu využijeme Clausiovu–Clapeyronovu rovnici, která popisuje změnu tlaku s teplotou během fázového přechodu. Tato rovnice má tvar
\[\frac{dp}{dT} = \frac{L_\mathrm{t}}{TΔV},\]kde Lt je skupenské teplo tání ledu, T je teplota tání ledu a ΔV je změna objemu po roztátí ledu.
Zajímá nás, jak se změní teplota tání ledu, jestliže na led tlačí struna, na které je zavěšeno závaží. Změnu teploty zjistíme ze vztahu
\[dT = dp\frac{TΔV}{L_\mathrm{t}}.\tag{1}\]Pro výpočet změny teploty tání potřebujeme nejdříve zjistit, jaká bude změna tlaku dp na led, jestliže je na něj zavěsíme strunu se závažím. Tlak struny p na led vypočítáme jako
\[p = \frac{F}{S} = \frac{mg}{ld},\]kde m je hmotnost závaží zavěšeného na struně, l je průměr ledu v místě, na které tlačí struna, a d je průměr struny. Dosadíme do vztahu zadané hodnoty
\[p = \frac{6{,}5·9{,}8}{5{,}6·10^{−2}·2{,}4·10^{−4}} \mathrm{Pa}.\]Tlak struny se závažím na led má přibližně velikost
\[p \dot{=} 4{,}74·10^{6} \mathrm{Pa}.\]Po zavěšení struny se tedy tlak na led zvýší o tlak struny p. Změna tlaku na led dp tak bude mít velikost
\[dp \dot{=} 4{,}74·10^{6} \mathrm{Pa}.\]Dále potřebujeme znát změnu objemu při roztání ledu. Určíme ji jako rozdíl objemu vody VV a objemu ledu VL o stejné hmotnosti 1 kg
\[ΔV = V_\mathrm{V}−V_\mathrm{L} = \frac{m_\mathrm{V}}{ρ_\mathrm{V}}−\frac{m_\mathrm{L}}{ρ_\mathrm{L}}.\]Nyní můžeme dosadit do vztahu (1) a dopočítat, jak se změní teplota tání ledu
\[dT = dp\frac{TΔV}{l_\mathrm{t}} = p\frac{T(\frac{m_\mathrm{V}}{ρ_\mathrm{V}}−\frac{m_\mathrm{L}}{ρ_\mathrm{L}})}{L_\mathrm{t}}.\]Po dosazení dostáváme
\[dT \dot{=} 4{,}74·10^{6}\frac{373{,}15·(\frac{1}{999{,}8}−\frac{1}{916{,}8})}{3{,}34·10^{5}} °\mathrm{C}\] \[dT \dot{=} −0{,}48 °\mathrm{C}.\]V podmínkách, při kterých probíhalo naše měření, klesla teplota tání ledu pod zatíženou strunou přibližně o 0,48 °C.








