Sbírka fyzikálních pokusů

Pohlcování tepelného záření plastovými filtry

Pokus číslo: 1743

• Cíl pokusu

  Cílem experimentu je proměřit, jak je tepelné záření emitované předmětem zeslabováno při průchodu plastovými filtry.

• Teorie

  Experiment, který níže popíšeme, je založen na práci s termovizní kamerou. Principem termovizních měření je detekce záření emitovaného studovaným tělesem. Pokud termovizní kamera vyhodnotí intenzitu emitovaného záření \(I\) \(([I]\,=\,\mathrm{W{\cdot}m^{-2}})\), můžeme pak povrchovou teplotu T předmětu o emisivitě ε odhadnout ze Stefanova-Boltzmannova zákona:

  \[I\,=\,{\epsilon}{\sigma}T^4\tag{1}\]

  kde σ je Stefanova-Boltzmannova konstanta.

  Vztah (1) je určitým zjednodušením skutečné situace – zaprvé předpokládá, že měřený objekt lze modelovat tzv. šedým tělesem, tj. tělesem s emisivitou nezávislou na frekvenci emitovaného záření, zadruhé zanedbává záření atmosféry a vlastní záření čipu termokamery, které jsou při vyhodnocování teploty měřeného objektu také brány v potaz a korigovány.

  Pokud emitované záření o počáteční intenzitě \(I_0\) prochází materiálem tloušťky d, je v něm pohlcováno a jeho intenzita exponenciálně klesá v závislosti na tloušťce materiálu podle vztahu:

  \[I(d)\,=\,I_0e^{-\beta d}\tag{2}\]

  kde β je tzv. absorpční koeficient charakterizující materiál. Vztah (2) bývá označován jako Lambertův-Beerův zákon a častěji se s ním setkáváme při průchodu viditelného světla roztoky různých látek.

  Dosazením vztahu (2) do vztahu (1) získáváme teoreticky odvozený průběh teploty měřené termovizní kamerou ve tvaru:

  \[{\epsilon}{\sigma}T^4\,=\,{\epsilon}{\sigma}T_0^4e^{-\beta d}\tag{3}\] \[T\,=\,T_0\sqrt[4]{e^{-\beta d}}\tag{4}\]

  Úpravou rovnice (4) pak můžeme vyjádřit očekávanou závislost teploty měřené termovizní kamerou na tloušťce materiálu d, který mezi kameru a zdroj záření vložíme:

  \[T(d)\,=\,T_0{e^{-{\frac{1}{4}}\beta d}}\tag{5}\]

  Podobně jako v případě intenzity záření bychom tedy měli očekávat exponenciální pokles měřené teploty. Různou tloušťku materiálu d budeme v našem experimentu realizovat zvyšováním počtu plastových folií umístěných mezi zdroj záření a termovizní kameru.

  Cílem uvedeného odvození bylo ukázat skutečnost, že naměřená hodnota teploty klesá s tloušťkou pohlcujícího materiálu skutečně exponenciálně. Je opět potřeba brát toto odvození jako idealizované, ilustrační – například je zřejmé, že při zvyšování tloušťky materiálu k nekonečnu se měřená teplota rozhodně nebude blížit hodnotě 0 K, jak by teoretický model napovídal. Intenzita prošlého záření sice k nule poklesne, ale více se začne projevovat vlastní tepelné záření pohlcujícího materiálu (v našem případě vkládaných filtrů), které způsobí, že exponenciála popisující teplotní vývoj se bude asymptoticky blížit nikoliv absolutní nule, ale pokojové teplotě.

• Pomůcky

  Termovizní kamera, plastové filtry (cca 10 ks), předmět o znatelně vyšší teplotě, než je teplota okolí.

  V konkrétním vzorovém experimentu byla jako předmět emitující tepelné záření použita žárovka o výkonu 60 W, jejíž povrch se po cca 10 minutách provozu téměř ustálil na teplotě kolem 180 °C.

  Filtry velikosti cca 4x5 cm (obr. 1) byly vystříhány z polypropylenového obalu na CD/DVD; podobně by bylo možné k jejich výrobě použít např. euroobaly. Jediným požadavkem na použitý plast je, aby nepohlcoval příliš mnoho záření – umístění jednoho či dvou filtrů by v takovém případě zabránilo průchodu veškerého infračerveného záření a dále by nebylo co měřit. Z tohoto důvodu nelze použít například filtry vyrobené z PET lahví, naopak doporučit lze právě polypropylen či polyethylen.

  

• Postup

  1. Termovizní kameru zafixujeme vůči studovanému předmětu tak, aby sledovala stále stejné místo. Ve vzorovém měření byla vzdálenost mezi kamerou a předmětem přibližně 120 cm.

  2. Poznamenáme si teplotu, kterou kamera měří, není-li před ni vložen žádný filtr.

  3. Vložíme jeden filtr a zapíšeme měřenou teplotu. Postup opakujeme pro postupně se zvyšující množství filtrů; je vhodné proměřit alespoň osm hodnot.

• Vzorový výsledek

  Hodnoty naměřené ve vzorovém experimentu jsou uvedeny v tabulce níže:

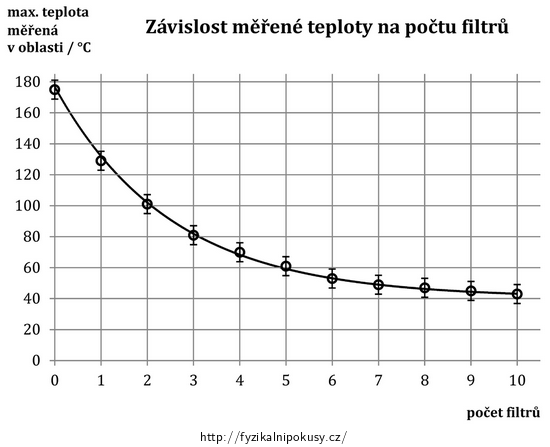
  počet filtrů	0	1	2	3	4	5	6	7	8	9	10
  měřená teplota (°C)	175	129	101	81	70	61	53	49	47	45	43

  Graficky jsou uvedené hodnoty zpracovány do grafu na obr. 2 a je jimi proložena exponenciální závislost:

  

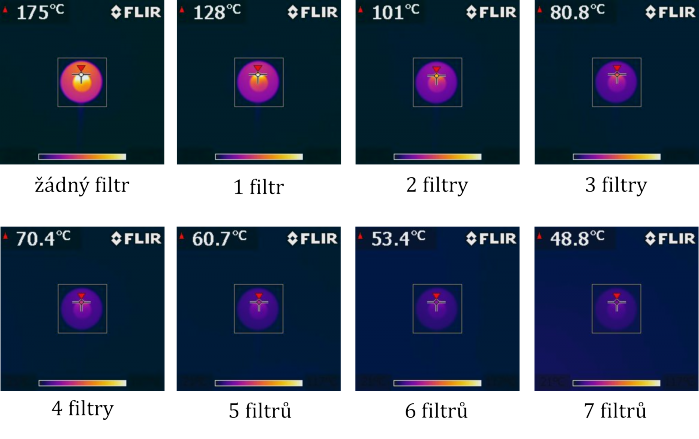
  Alternativně lze pokles měřené teploty vyjádřit přímo snímky z termovizní kamery - viz obr. 3.

  

  Při přípravě obr. 3 byla použita termovizní kamera FLIR i7, teplotní rozsah škály barev byl zvolen v intervalu 21 °C až 117 °C, emisivita ε = 0,95. Kamera přitom pracovala v režimu maximálních hodnot, kdy udávala vždy nejvyšší teplotu naměřenou v bíle orámovaném čtverci (odtud označení svislé osy ve výše uvedeném grafu).

• Technické poznámky

  • Pokud chceme používat při experimentování stejně jako ve vzorovém pokusu žárovku, je třeba nechat ji cca 10 minut před začátkem měření svítit, aby se její povrchová teplota přibližně ustálila. Toto ustálení sice není ani po 10 minutách dokonalé, ale růst teploty je již tak pomalý, že měřenou exponenciální závislost nijak nenaruší. Rozhodně ale není možné zahájit měření krátce po rozsvícení žárovky, kdy její teplota ještě strmě roste; obecně potřebujeme použít těleso s přibližně konstantní povrchovou teplotou.

  • Jiný způsob, jakým můžeme realizovat plastové filtry, je použít jako základní jednotku čtvereček izolepy a postupným nalepováním dalších a dalších vrstev zvyšovat tloušťku pohlcujícího materiálu.

• Metodické poznámky

  • Pro ještě názornější pojetí experimentu může být vhodné použití takového studovaného předmětu, který nevydává viditelné světlo – aby bylo studentům skutečně jasné, že to, co termokamerou detekujeme a filtry zeslabujeme, je právě tepelné infračervené záření. Předmětem, který viditelné světlo nevydává a současně si drží přibližně konstantní teplotu výrazně vyšší než je teplota okolí, může být například rychlovarná konvice s vroucí vodou a otevřeným víkem (to zajistí, že se konvice navzdory varu vody nevypne).

  • Můžeme se studenty diskutovat o tom, zda není problémem to, že jsme vztah (5) odvodili pro termodynamickou teplotu, ale graf na obr. 2 je vynesen pro teplotu Celsiovu. Studenti poměrně snadno přijdou na to, že v případě termodynamické teplotní stupnice by se celý graf pouze posunul po svislé ose.

  • Je třeba vnímat odvozený vztah (5) skutečně jen jako první přiblížení skutečné situace – v reálu termovizní kamery pracují s komplikovanějším matematickým vztahem, filtry část záření odrážejí atd.

• Základy práce s termovizní kamerou - odkaz na PDF

  Tento experiment využívá termografické měření. Dokument Experimentujeme s termovizní kamerou shrnuje teorii termografie a základní doporučení a postupy, které mohou napomoci k přesnějším a nezkresleným výsledkům měření.