Sbírka fyzikálních pokusů

Určení měrného skupenského tepla varu vody

Pokus číslo: 1620

• Cíl pokusu

  Zatímco určování měrného skupenského tepla tání ledu (resp. tuhnutí vody) bývá poměrně běžným praktickým úkolem středoškoláků, měrné skupenské teplo varu často zmiňujeme pouze teoreticky. Tento experiment umožňuje jeho snadné a poměrně přesné určení v čase ne delším než 15 minut. Ideou měření je využití konstantního tepelného výkonu rychlovarné konvice při ohřívání i varu vody.

• Teorie

  K tomu, abychom vodu o hmotnosti m₁ v rychlovarné konvici ohřáli o rozdíl teplot Δt, je třeba jí dodat teplo

  \[Q\,=\,cm_1{\Delta}t,\tag{1}\]

  kde konstanta c je měrná tepelná kapacita vody, c = 4180 J·kg⁻¹·K⁻¹. Pokud navíc víme, že zvýšení teploty o Δt si vyžádalo čas τ₁, můžeme určit průměrný tepelný výkon P₁ konvice při ohřevu jako

  \[P_1\,=\,\frac{Q}{{\tau}_1}\,=\,\frac{cm_1{\Delta}t}{{\tau}_1}.\tag{2}\]

  Při dosažení teploty varu se přestává teplota kapaliny zvyšovat a veškeré dále dodávané teplo je využíváno na vypařování kapaliny z celého jejího objemu. Toto teplo označujeme jako skupenské teplo varu L_v. Dodání většího tepla L_v umožní změnu skupenství většímu množství vody m₂, což lze matematicky vyjádřit jako

  \[L_\mathrm{v}\,=\,m_2l_\mathrm{v},\tag{3}\]

  kde m₂ je hmotnost varem odpařené vody. Konstanta úměrnosti l_v se nazývá měrné skupenské teplo varu a udává teplo, které je třeba dodat jednomu kilogramu kapaliny (zde vody) zahřáté na teplotu varu, aby se tato zcela přeměnila na páru stejné teploty. Pokud navíc víme, že se voda o hmotnosti m₂ odpařila za čas τ₂, můžeme určit průměrný tepelný výkon P₂ konvice při varu jako

  \[P_2\,=\,\frac{m_2l_\mathrm{v}}{\tau_2}.\tag{4}\]

  Budeme-li nyní předpokládat, že tepelný výkon konvice je během ohřevu vody i během jejího varu stejný (lze ověřit například použitím wattmetru), tj. P₁ = P₂, dostáváme rovnost výkonů ve tvaru:

  \[\frac{cm_1{\Delta}t}{\tau_1}\,=\,\frac{m_2l_\mathrm{v}}{\tau_2}.\tag{5}\]

  Z této rovnice již snadno vyjádříme hledané měrné skupenské teplo varu vody jako

  \[l_\mathrm{v}\,=\,c{\Delta}t\frac{m_1}{m_2}\frac{\tau_2}{\tau_1}.\tag{6}\]

• Pomůcky

  Teploměr (výhodou, ale ne podmínkou je čidlo spolupracující s počítačem, které je schopné vykreslovat časový vývoj teploty; pro tento konkrétní experiment bylo využito čidlo Vernier Go!Temp), rychlovarná konvice, váhy (postačuje citlivost 1 g).

• Postup

  Konvici naplníme přibližně do poloviny jejího maximálního deklarovaného objemu studenou kohoutkovou vodou a zvážíme ji. Upevníme teploměr tak, aby měřil teplotu několik centimetrů pod hladinou, ale současně se nedotýkal topné spirály či dna konvice. Víko konvice necháváme po celou dobu experimentu otevřené.

  Současně se zapnutím konvice spustíme měření teploty. Přivedeme vodu k varu a poté ji necháme – stále při otevřeném víku – vřít alespoň po dobu srovnatelnou s dobou ohřevu, event. déle. Následně ukončíme měření teploty, současně vypneme konvici a co nejrychleji ji opět zvážíme. Z rozdílu hmotností před a po experimentu zjistíme hmotnost m₂ vyvařené vody. Na závěr vodu vylijeme a zvážíme konvici prázdnou – to nám umožní dopočítat původní hmotnost vody m₁.

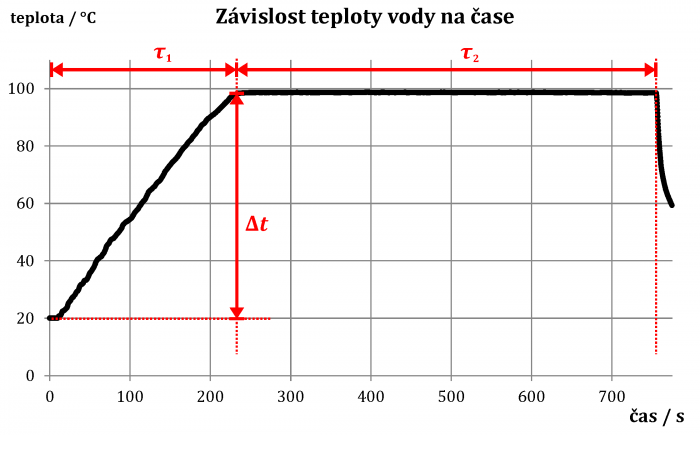
  Všechny ostatní údaje, tj. Δt, τ₁ a τ₂ vyčteme z naměřené závislosti teploty na čase – viz příklad měření na obr. 1.

  

• Vzorový výsledek

  Pro ilustraci jsou v tabulce níže přiloženy výsledky pěti měření. Průměrná hodnota měrného skupenského tepla varu vody l_v vzešlá z těchto pěti měření činí přibližně 1,94 MJ·kg⁻¹, což představuje odchylku asi 14 % od tabulkové hodnoty (2,26 MJ·kg⁻¹). Chyby měření jsou diskutovány níže.

  měření	m1/kg	m2/kg	τ1/s	τ2/s	Δt/°C	lv/MJ·kg−1
  1	0,470	0,176	225	520	78,5	2,03
  2	0,476	0,106	230	310	78,0	1,97
  3	0,429	0,097	201	280	73,5	1,90
  4	0,414	0,082	200	237	77,1	1,93
  5	0,363	0,123	183	362	77,0	1,88
  průměr	-	-	-	-	-	1,94

• Limity měření

  • Největším zdrojem chyb v tomto experimentu je předpoklad, že během ohřevu vody se tepelný výkon konvice využije pouze na ohřev vody – ve skutečnosti se musí ohřát také vlastní tělo konvice, které v tomto konkrétním případě se svojí hmotností téměř 350 g vstupuje do tepelné bilance poměrně výrazně. Kdyby se nemuselo ohřívat i tělo konvice, byl by čas τ₁ kratší, dopočítaná hodnota l_v by vzrostla a více se blížila své skutečné hodnotě.

  • Další nepřesností je předpoklad, že vzniklá pára konvici zcela opouští. Ve skutečnosti její část kondenzuje na stěnách konvice, stéká zpět a může tak být „odpařena dvakrát“. Jinak řečeno, hmotnost skutečně odpařené vody m₂ je větší než pouhý rozdíl hmotností vody před a po experimentu. Tuto nepřesnost lze alespoň minimalizovat tím, že použijeme konvici, která se směrem vzhůru nijak zásadně nezužuje. Pozor! S konvicemi, které mají ústí výrazně zúžené, můžeme dostat velmi špatné výsledky (i s více než padesátiprocentní odchylkou od skutečné hodnoty).

  • Výše uvedené chyby se svým vlivem na vypočtenou hodnotu měrného skupenského tepla varu vzájemně částečně kompenzují.

  • V experimentu dále neuvažujeme, že voda se vypařuje za každé teploty, tedy i během svého ohřevu na teplotu varu; tento vliv je ovšem slabý.

• Další technické poznámky

  • Je opravdu důležité, aby nebyla konvice plná více než z poloviny předepsaného objemu. V opačném případě začne během varu voda cákat mimo konvici a kromě znehodnocení měření tak může způsobit i opaření experimentátorů. Je vhodné před měřením optimální výšku hladiny vyzkoušet a během měření dodržovat zásady bezpečnosti práce s vroucí vodou.

  • Teploměr musí být ponořený do hloubky několika centimetrů, aby nedošlo k tomu, že během měření se s úbytkem vody dostane jeho měřicí část nad hladinu.

• Metodické poznámky

  • Experiment lze využít k tomu, aby žáci lépe porozuměli grafům souvisejícím se změnami skupenství, se kterými se na základoškolské i středoškolské úrovni setkávají. Zejména je třeba zdůraznit, že v našem měření nejde o tvarově shodný graf závislosti dodaného tepla na čase, který obvykle figuruje v učebnicích, ale o závislost teploty na čase.

  • Průběh experimentu lze využít také ke konfrontaci studentů s jednou z nejsilnějších a neodolnějších miskoncepcí, které byly v termodynamice identifikovány. Studenti bývají velmi silně přesvědčeni, že při kontinuálním varu vody její teplota nutně překročí 100 °C. Graf na obr. 1 přitom může sloužit jako jasný protipříklad – ačkoliv vodě dodáváme teplo několik minut, její teplota zůstává při varu konstantní a nad 100 °C nevystoupí.