Závislost tlaku syté vodní páry na teplotě
Pokus číslo: 1672
Cíl pokusu
Cílem experimentu je proměřit závislost tlaku syté vodní páry na teplotě v rozmezí přibližně 35 °C až 85 °C.
Teorie
Skupenská přeměna kapaliny na její sytou páru patří mezi fázové přechody 1. druhu, tedy takové procesy, při kterých látka mění svůj molární objem a molární entropii. Jednodušeji řečeno, látka stálé hmotnosti při takovémto fázovém přechodu změní svůj objem a přijme/odevzdá tzv. latentní teplo, jež ale souvisí pouze se změnou její fáze, nikoliv se změnami teploty. Je-li uvedený fázový přechod skupenskou přeměnou, označujeme toto latentní teplo obvykle jako skupenské teplo Qsk, při přepočtení na 1 mol látky jako molární skupenské teplo qsk.
Matematický popis fázových přechodů 1. druhu poskytuje Clausiova-Clapeyronova rovnice, kterou lze odvodit z hlavních termodynamických vět například ve tvaru:
\[\frac{\mathrm{d}p}{\mathrm{d}T}\,=\,\frac{{\Delta}S_m}{{\Delta}V_m},\tag{1}\]kde derivace tlaku podle termodynamické teploty \(\frac{\mathrm{d}p}{\mathrm{d}T}\) je myšlena podél křivky koexistence dvou fází, ΔSm je změna molární entropie a ΔVm změna molárního objemu.
Pomocí výše zmíněného molárního skupenského tepla qsk a termodynamické teploty T lze rovnici (1) přepsat ve tvaru
\[\frac{\mathrm{d}p}{\mathrm{d}T}\,=\,\frac{q_{sk}}{T{\Delta}V_m}\,=\,\frac{q_{sk}}{T(V_{m2}\,-\,V_{m1})}\tag{2}\]Pokusíme se nyní odvodit závislost tlaku syté páry na termodynamické teplotě. Pokud jde o skupenskou přeměnu kapaliny (molární objem \(V_{m1}\)) na její sytou páru (molární objem \(V_{m2}\)), můžeme s rozumnou přesností uplatnit dvě zanedbání:
Předně, molární objem kapaliny \(V_{m1}\) je zřejmě mnohem menší než molární objem páry \(V_{m2}\), tedy \(V_{m2}\,-\,V_{m1}\,\doteq\,V_{m2}\); dále budeme \(V_{m2}\) označovat jednoduše jako \(V_{m}\). Rovnice (2) tak získává tvar:
\[\frac{\mathrm{d}p}{\mathrm{d}T}\,=\,\frac{q_{sk}}{TV_m}\tag{3}\]Dále, páru budeme modelovat ideálním plynem popsaným stavovou rovnicí
\[pV\,=\,nRT\tag{4}\]kde n je látkové množství a R molární plynová konstanta. Z rovnice (4) přímo plyne:
\[V_m\,=\,\frac{RT}{p}\tag{5}\]
Spojením vztahů 3 a 5 dostáváme:
\[\frac{\mathrm{d}p}{\mathrm{d}T}\,=\,\frac{pq_{sk}}{RT^2}\tag{6}\]Rovnici 6 převedeme na tvar se separovanými proměnnými a obě strany integrujeme:
\[\int_p{\frac{\mathrm{d}p}{p}}\,=\,\int_T{\frac{q_{sk}}{R}\frac{\mathrm{d}T}{T^2}}\tag{7}\]Pro qsk nezávislé na teplotě získáváme řešení rovnice (7) ve tvaru:
\[\ln{p}\,=\,A\,{-\frac{q_{sk}}{RT}},\tag{8}\]kde A je integrační konstanta. Tlak p tedy zřejmě závisí exponenciálně na reciproké teplotě; ačkoliv jsme tedy částečně vyšli z modelu ideálního plynu, dostáváme pro sytou páru jiný vztah mezi tlakem a teplotou, než jaký udává pro ideální plyn Gay-Lussacův zákon.
Pomůcky
Převařená destilovaná voda; kádinka alespoň 0,5 l; aparatura pro určování molárního skupenského tepla vypařování vody (obr. 1, výrobce: PHYWE).
Postup
A. Příprava měření:
Experimentální baňku naplníme přibližně ze tří čtvrtin jejího objemu převařenou destilovanou vodou (tj. vodou odplyněnou a deminerazilovanou).
Na ohřívací plotnu postavíme kádinku o objemu alespoň 0,5 litru a na její dno vložíme magnetickou míchací tyčinku.
Experimentální baňku upevníme tak, aby byla co nejvíce zanořena do kádinky.
Kádinku naplníme obyčejnou vodou tak, aby byla experimentální baňka co nejvíce ponořená; kádinka bude pro experimentální baňku představovat vodní lázeň.
Podle obrázku 2 zavedeme do experimentální baňky trubici od manometru (otvor vpravo), hadici od vývěvy (otvor uprostřed) a teploměr (otvor vlevo). Zatímco teploměr do převařené destilované vody ponoříme, obě skleněné trubice musí zůstat dostatečně vysoko nad ní.
S citem utáhneme všechny červené šroubovací uzávěry.
B. Kalibrace manometru
V tomto experimentu budeme používat manometr, který se při měření tlaku naplní vodou. Po naplnění vodou tedy může ukazovat jinou hodnotu, než je hodnota atmosférického tlaku, přestože bude jeho vývod volně spojen s okolním vzduchem. Úkolem kalibrace je zjistit, jak velká je tato odchylka.
Zkontrolujeme, zda je skleněný kohout otevřený, a pomocí vývěvy vyčerpáme vzduch z experimentální baňky. Pak kohout uzavřeme a vývěvu vypneme.
Trubici vedoucí k manometru zasuneme pod hladinu destilované vody, skleněný kohout opět otevřeme a otočením zavzdušňovacího kohoutu vývěvy (obr. 3) napustíme do experimentální baňky vzduch. V důsledku toho je část vody z baňky vtlačena do trubice manometru i do manometru samotného.

Barometrem změříme atmosférický tlak pa v místnosti a poznamenáme si ho.
Zapneme míchání (například 900 otáček za minutu) a začneme zahřívat; vařič můžeme nastavit (obr. 4) například na teplotu 250 °C.

Když voda v experimentální baňce dosáhne teploty 35 °C (měřeno kapalinovým teploměrem uvnitř baňky), vysajte z baňky vzduch, uzavřete skleněný kohout a poznamenejte si tlak p0 měřený manometrem. Teprve nyní jste připraveni měřit!
C: Vlastní měření:
Dále zahřívejte. Pro teplotu 40 °C si poznamenejte tlak měřený manometrem a totéž pak s krokem 5 °C opakujte až do teploty 85 °C.
Vypněte vařič, otevřete zavzdušňovací kohout vývěvy a zpracujte naměřená data.
Vzorový výsledek: Naměřená data
Vzhledem k tomu, jakým způsobem je ocejchován používaný manometr (obr. 5), získáváme odečtem z jeho stupnice pro vyšší teploty nižší hodnoty tlaku (v tabulce 1 označené jako pman).

Abychom získali skutečné hodnoty tlaku pskut, musíme zohlednit aktuální atmosférický tlak pa a také tlak p0 vodního sloupce v manometru, určený při kalibraci. Převod se řídí vztahem:
\[p_{skut}\,=\,p_a\,-(\,p_{man}\,-\,p_0)\,=\,p_a\,-\,p_{man}\,+\,p_0\]V případě konkrétního vzorového měření byly přibližné hodnoty \(p_a\,\doteq\,98\,\mathrm{kPa}\), resp. \(p_0\,\doteq\,4\,\mathrm{kPa}\). Tabulka níže udává naměřené hodnoty závislosti tlaku na teplotě.
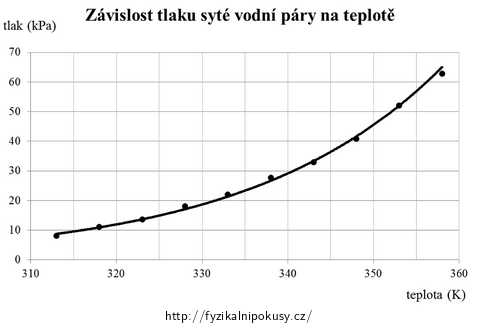
t (°C) T (K) pman (kPa) pskut (kPa) 40 313 94 8 45 318 91 11 50 323 88 14 55 328 84 18 60 333 80 22 65 338 74 28 70 343 69 33 75 348 61 41 80 353 50 52 85 358 39 63 Vzorový výsledek: Zpracování naměřených dat
Graficky jsou data znázorněna na obr. 6, tlak na ose y představuje v tabulce uváděný tlak pskut.
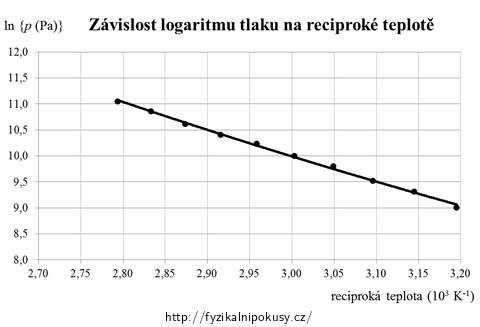
Přínosnější je ovšem vynést hodnoty do grafu, který by lépe odpovídal rovnici (8) - tj. takového, na jehož svislou osu se bude vynášet \(\ln{p}\) a na vodorovnou osu reciproká termodynamická teplota \(\frac{1}{T}\) (viz obr. 7).
Výhodnost grafu na obr. 7 je v tom, že naměřené hodnoty v něm lze snadno proložit lineární závislostí danou vztahem (8); tu můžeme zapsat v obecném tvaru jako
\[\ln{p}\,=\,A\,-\,\frac{B}{T},\tag{9}\]kde A a B jsou konstanty; rovnice (9) bývá označována jako tzv. Augustova rovnice. V tomto konkrétním případě má regresní přímka tvar:
\[\ln{\{p\}}\,=\,25\,-\,\frac{4{,}99{\cdot}10^3\,\mathrm{K}}{T}.\tag{10}\]Z hlediska určení molárního skupenského tepla vypařování vody je pro nás podstatná hodnota \(B\,=\,4{,}99{\cdot}10^3\,\mathrm{K}\), pro kterou porovnáním vztahů (8) a (9) dostáváme:
\[B\,=\,\frac{q_{sk}}{R}.\tag{11}\]Odtud pak již přímo plyne:
\[q_{sk}\,=\,BR.\tag{12}\]Pro číselné hodnoty získáváme z našeho experimentu:
\[q_{sk}\,=\,4{,}99{\cdot}10^3\,{\cdot}\,8{,}31\,\mathrm{J{\cdot}mol^{-1}}\,\doteq\,41{,}5\,\mathrm{kJ{\cdot}mol^{-1}}.\]Pro srovnání, tabulková hodnota molárního skupenského tepla vypařování vody je 44,2 kJ/mol při teplotě 20 °C a 40,6 kJ/mol při teplotě 100 °C.
Technické poznámky
Jak už bylo uvedeno výše, je nezbytné používat při experimentu důkladně převařenou destilovanou vodu (je vhodné nechat ji vařit cca 15 minut).
Pokud začne destilovaná voda v experimentální baňce po spuštění vývěvy v celém svém objemu probublávat, ihned vývěvu vypněte – taková voda nebyla dostatečně odplyněna.
Zejména při zasouvání skleněných trubiček do experimentální baňky je třeba postupovat velmi opatrně, aby nedošlo k poškození křehkých skleněných částí.
Dodržujte zásady bezpečné práce s vařičem. Během experimentu bude mít jeho plotna teplotu cca 250 °C! Podobnou obezřetnost vyžaduje manipulace s vodní lázní pro experimentální baňku; její teplota se v závěru experimentu blíží 90 °C.
Metodické poznámky
Protože v našem experimentu používáme hned v jeho úvodu převařenou destilovanou vodu pokojové teploty, je velmi rozumné si takovou vodu připravit ještě před začátkem měření (třeba s hodinovým předstihem). Pokud tak neučiníme, pravděpodobně nás převáření a následné chladnutí vody obere o desítky minut cenného času.